Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

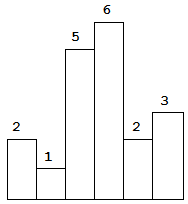
Histogram

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

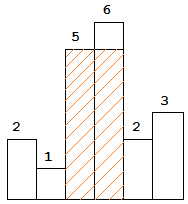
Histogram_area

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example, Given heights = [2,1,5,6,2,3], return 10.

Solution_1

　　如果不限制时间复杂度的话，O(n^2)的时间复杂度可以很容易实现代码。

之前的一个比较简单的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int largestRectangleArea(int[] height) {
    if (height == null || height.length <= 0) return 0;
    int maxArea = 0;
    for (int i = 0; i < height.length; i++) {
        int minHeight = height[i];
        for (int j = i; j < height.length; j++) {
            if (height[j] < minHeight) {
                minHeight = height[j];
            }
            int tempArea = minHeight * (j - i + 1);
            if (tempArea > maxArea) {
                maxArea = tempArea;
            }
        }
    }
    return maxArea;
}

　　即最直接的思路，考虑所有可能的window，然后找出最小高度，然后计算面积。显然，O(n^2)的时间复杂度不能AC。

Solution_2

　　然后借鉴水中的鱼-[LeetCode] Largest Rectangle in Histogram 解题报告，采用stack来进行计算，使得时间复杂度降低到O(n)。

  1. 初始化Stack<Integer> stack，并在数组末尾添加0。
  2. 遍历数组，如果当前数字大于stack.peek(), 则将顶端数字pop出来，并计算面积大小与maxArea取最大，直到顶端数字小于当前数字。
  3. 返回maxArea。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
   public int largestRectangleArea(int[] height) {
        Stack<Integer> stack = new Stack<Integer>();
        int[] h = new int[height.length + 1];
        h = Arrays.copyOf(height, height.length + 1);
        
        int i = 0; 
        int maxArea = 0;
        while(i < h.length){
            if(stack.isEmpty() || h[i] >= h[stack.peek()])
                stack.push(i++);
            else{
                int temp = stack.pop();
                maxArea = Math.max(maxArea, h[temp]*(stack.isEmpty()?i:(i-stack.peek()-1)));
            }
        }
        return maxArea;
   }
}

　　大致思路为：当数组为递增的时候，如[1,2,3,4,5]，类似这种的时候，我们其实可以直接计算1x5, 2x4, 3x3, 4x2, 5x1,然后比较最大即可。

　　以上的算法即为不断的找出递增数列然后计算面积的过程。通过上述算法虽然AC，但是时间27 ms，只能beat 30%左右，究其原因，是test case中存在大量的递增序列，导致算法本身O(2n)，比不上直接O(n).

可以稍加改进，增加如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
boolean sorted = true;
int l = height.length;
for (int i = 0; i < l; i++) {
   if (i > 0 && height[i] < height[i - 1]) 
      sorted = false;
}
if (sorted) {
   int max = 0;
   for (int i = 0; i < l; i++) {
      max = Math.max(max, height[i] * (l - i));
   }
   return max;
}

将特殊的test cases 特殊处理，AC，时间降低为6ms，beat92%。